Matematik
Modellering med sommerfugle og blomster
Introduktion I modellen oprettes et antal sommerfugle som flyver tilfældig omkring. Der er 9 blomster som står på rad og række. Når en sommerfugl er
Herunder finder du alle forløb i biblioteket. Brug søgefeltet for at udforske de forskellige forløb. Du kan også bruges vores grundbog til at få ny viden om teorier og metoder til din undervisning.
Mangler der et forløb i biblioteket? Upload dit eget forløb.
Menu
Matematik
Hældningsfelt og løsningskurver
Introduktion Kan tegne hældningsfelter i realtid (hver en parameter varieres med en skyder)Kan indsætte punkter i felter i realtid. Punkter følgende feltet og optegner løsningskurver
Fysik
Absorption af stråling
Introduktion Forløbet afvikles som begyndelse på et forløb om eksponentielle funktioner i matematik. Modellen er en simulering af absorption af fotoner i stof. Arbejdet med
Matematik
Differentialligninger, kombinatorik og statistisk fordeling
Introduktion Et antal personer bevæger sig tilfældigt rundt og knytter forbindelse når de er på samme position. Dette er modelleret som en simulation i NetLogo
Matematik
Simulering og terninger
Introduktion Modellen er tænkt som en måde at arbejde med simulering i en almindelig kendt matematisk situation. I modellen kan man slå med 3 –
Matematik
Matematisk modellering – kaninformering
Introduktion Dette forløb er lavet til 1.g. matematik med henblik på at træne modelleringstankegangen samt skabe egne datasæt til regressionsanalyse.Forløbet er bygget op af to
Matematik
Monty Hall
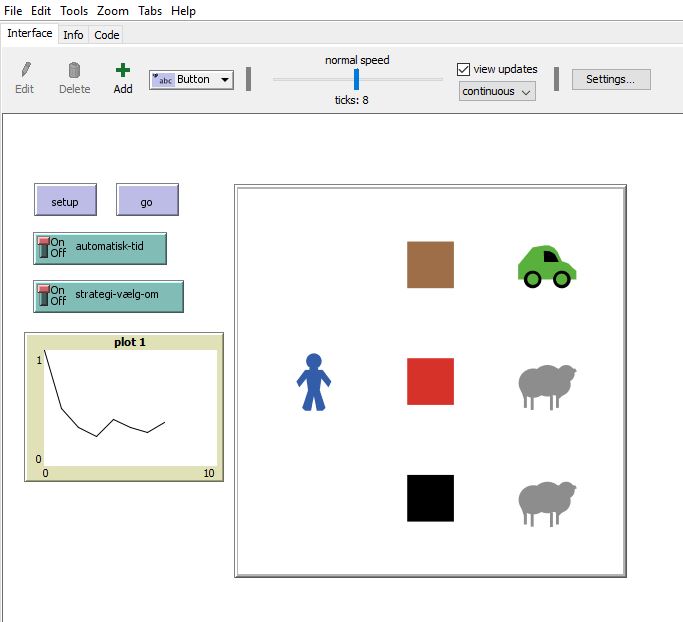
Introduktion CT aktiviteten blev brugt som indledning i forløbet om sandsynlighedsregning hvor vi får introduceret begreberne stokastisk variabel og sandsynlighed samt hører om emnet spilteori
Matematik
Kriminalitet
Introduktion I forløbet undersøger eleverne forskellige kriminalitetsteoriers forklaringskraft. Derudover arbejder eleverne med det danske retssystem, straffeformer, recidiv og resocialisering. Netlogo-modellen kan både bruges i starten af
Matematik
Væksttyper
Introduktion Modellen er tænkt som en første introduktion til væksttyper i matematikundervisningen i 1g. Modellen virker ved at lade et punkt bevæge sig med absolut
Matematik
SIR-modellen
Introduktion Dette er en model for, hvordan en sygdomsepidemi udvikler sig (SIR-modellen). Modellen er tænkt som et supplement til den traditionelle behandling af SIR-modellen med
Matematik
Parameterfremstilling og punktmængde
Introduktion Modellen er tænkt som en støtte i matematik undervisningen til forståelse af, at parameterfremstillingen beskriver en punktmængde der danner en linje. Overordnet beskrivelse af
Matematik
Lineær regression
Overordnet beskrivelse af aktiviteten Små sekvenser i diverse moduler under gennemgangen af kernestoffet lineær regression (mindste kvadraters metode) med black box Nspire/NetLogo. Der simuleres (i)
