Fang to punkter

–

Introduktion

Forløbet skal repetere og træne forståelsen af a og b for en lineær funktion og for en eksponentiel udvikling. Desuden skal eleverne efter forløbet kunne beregne a og b ud fra to punkter for begge typer af funktioner. Forløbet træner desuden eleverne i at tænke i algoritmer i deres CAS-program (her Nspire).

Aktivitetens længde

3 moduler (se flere detaljer i forløbsbeskrivelsen).

Materialer

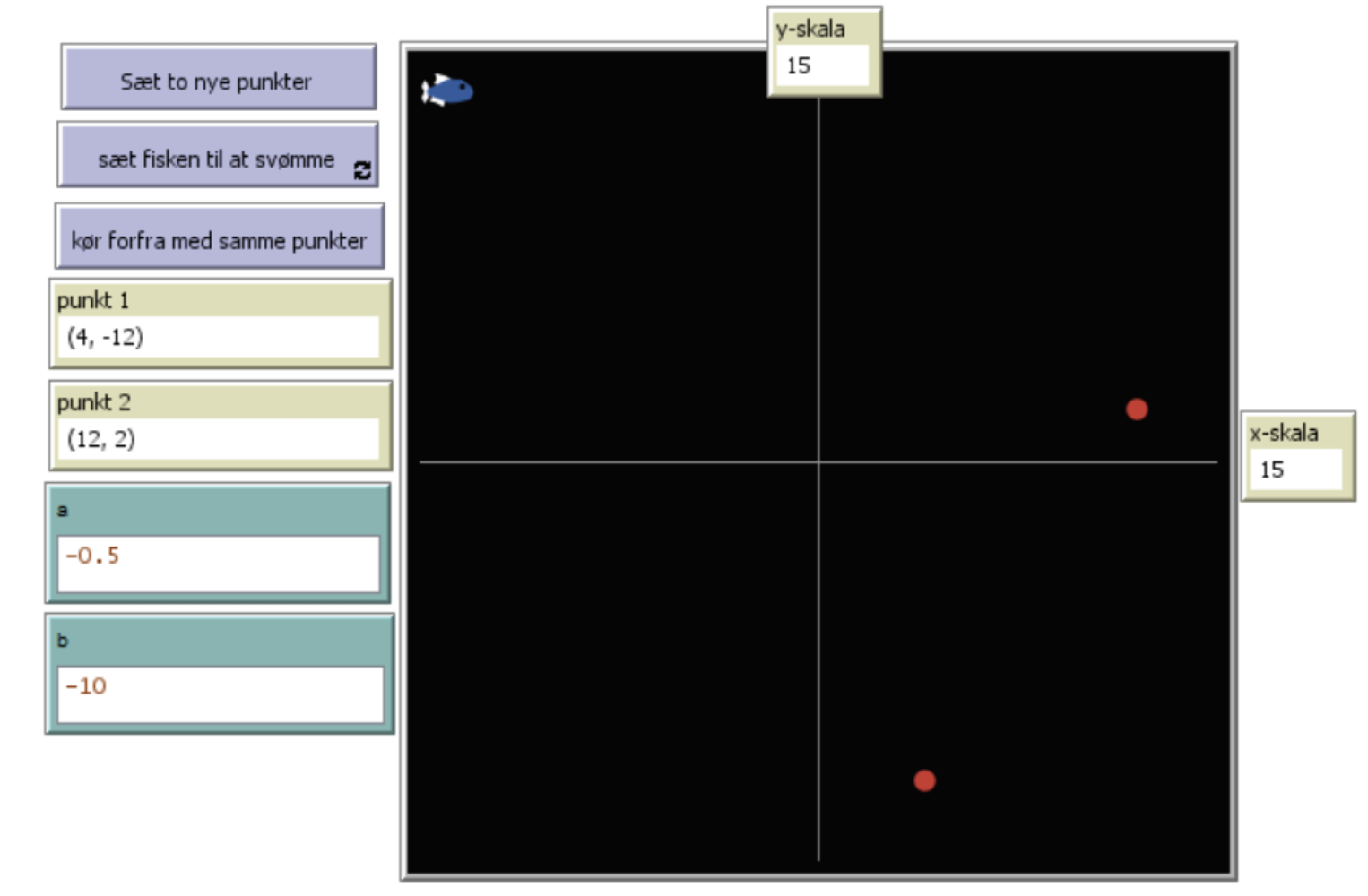
Når du downloader forløbs materialet, får du adgang til forløbets NetLogo-filer samt arbejdsark. Inden NetLogo-forløbet havde eleverne arbejdet med stoffet i Gyldendals Gymnasiematematik B-niveau. Eleverne fik filen ” jagt_efter_punkter_lineær.nlogo” som udgangspunkt. Denne fil generer to punkter med tilfældige heltalskoordinater og tegner en ret linje ud fra de brugervalgte værdier for a og b. Hvis linjen går gennem punkterne forsvinder de. Ud fra denne fil, skulle eleverne først træne at gætte a og b, og dernæst træne at beregne a og b. Derefter skulle eleverne selv ændre filen, så den kunne bruges til at tegne grafen for en eksponentiel udvikling. De skulle også ændre i designet, så punkterne blev ændret og fisken der trækker linjen skiftede farve eller var et andet dyr.

Aktivitetens sværhedsgrad

I kurset introducerede vi en model for sværhedsgraden af en CT-aktiviteten, hvor selve det modellerede stofs sværhedsgrad er på den lodrette akse, og i hvor høj grad eleverne skal arbejde med kode er på den vandrette akse. Elevernes arbejde i denne aktivitet er indtegnet. Det tog længere tid end forventet, at få eleverne klædt på til at have en algoritme i Nspire til den rette linje. Ambitionen var ikke så stor på NetLogo-delen fra min side. Jeg ville først og fremmest gerne have dem til at forstå formlernes generelle anvendelighed. Deres ”algoritme-karakter”. Det lykkedes formentlig ikke for alle, men de viste dog en del entusiasme til den afsluttende konkurrence.

Beskrivelse af aktiviteten

Forløbet var afsluttende op til juleferien, og var tænkt som kort opsamling på den rette linje gennem to punkter, og dernæst anvendelse af formlen for den eksponentielle udvikling gennem to punkter. Udover computational thinking med Netlogo, var det meningen at projektet skulle støtte ”algoritmetænkning” med Nspire, som er elevernes primære CAS-værktøj.

Afprøvning

1a Ma, Studieretning: Engelsk A, Samfundsfag A. 30 elever.

Forslag til forbedring

Der er mange muligheder for videre arbejde. En oplagt mulighed er naturligvis at prøve, om man kan fange to punkter med potensfunktioner eller fange tre punkter med en parabel. Layoutet kan forbedres med et gitter, så det er lettere at aflæse graferne. Man kunne også undlade at få punkternes koordinater vist, så man selv skal aflæse dem. Layoutet kan man naturligvis arbejde meget med. Det kan jo være et projekt i sig selv at tegne en spændende baggrund med parabler.