Matematik
Jagten på det logistiske dyr!
Introduktion Forløbet er tænkt som et længere afsluttende modelleringsforløb i differentialligninger, hvor særligt den logistiske populationsmodel sættes under kritisk lup. Overodnet går forløbet ud på
Herunder finder du alle forløb i biblioteket. Brug søgefeltet for at udforske de forskellige forløb. Du kan også bruges vores grundbog til at få ny viden om teorier og metoder til din undervisning.
Mangler der et forløb i biblioteket? Upload dit eget forløb.
Menu
Matematik
Geometriske steder
Introduktion Modellerne er tænkt som en introduktion til klassisk geometri, specifikt til geometriske steder. Udgangspunktet er definitionen af geometriske steder, som mængder af punkter –
Matematik
Fang to punkter
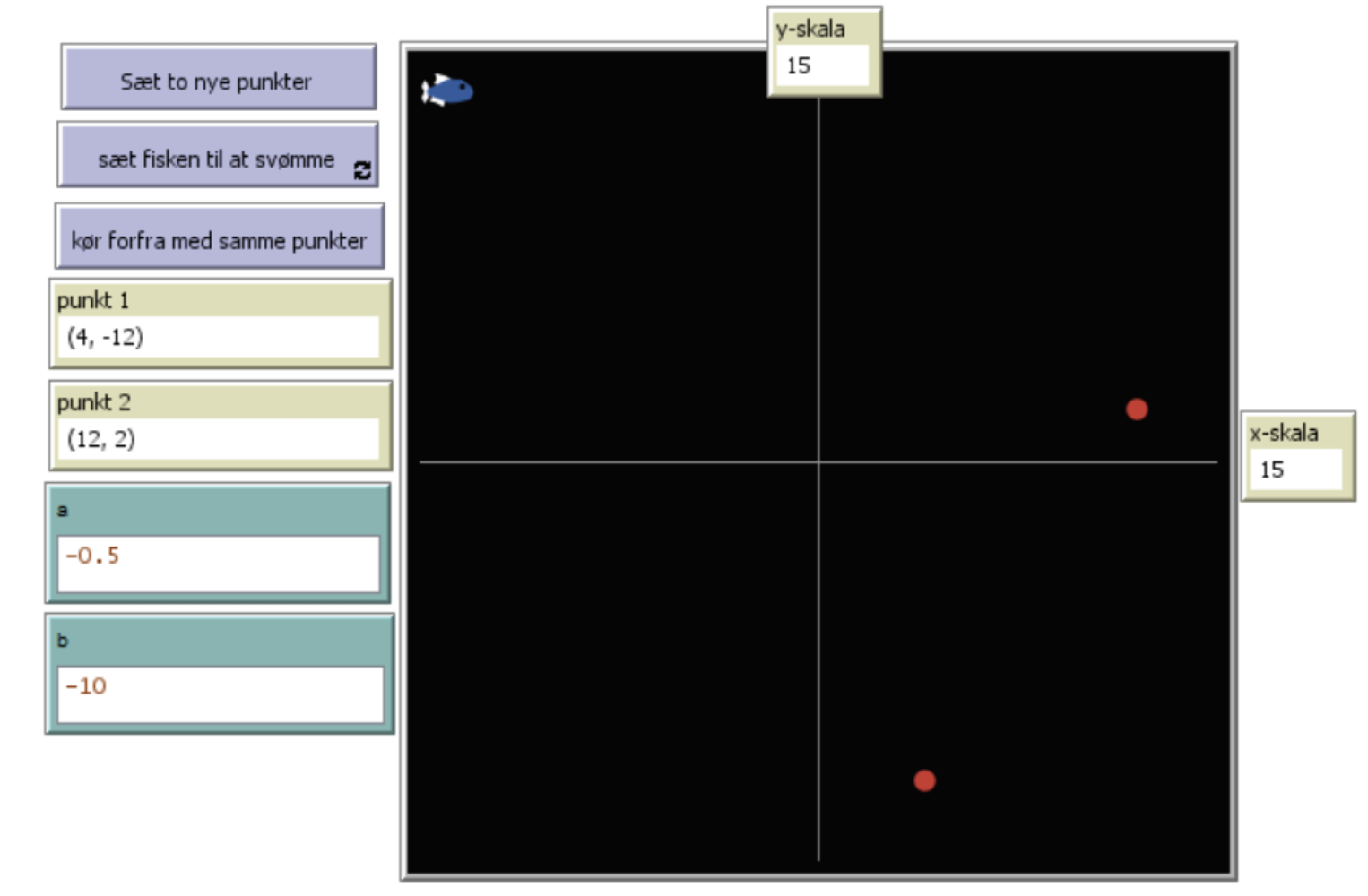
Introduktion Forløbet skal repetere og træne forståelsen af a og b for en lineær funktion og for en eksponentiel udvikling. Desuden skal eleverne efter forløbet
Matematik
Det lydløse terningekast
Introduktion Til forståelse af sandsynlighedsregning har kast med terninger altid haft en stor rolle. Men hvad er en terning? En terning er et lille objekt,
Matematik
Buffons nåleproblem
Introduktion Buffons nåleproblem omhandler spørgsmålet: Hvis vi kaster en nål på et gulv af brædder med samme bredde, hvad er da sandsynligheden for at nålen
Matematik
Simulering af binomialforsøg
Introduktion Modellen understøtter undervisningen i binomialfordelingen og konfidensintervaller. Modellen understøtter, at man skal gentage forsøget mange gange før man kan sige noget om sandsynligheden for
Matematik
Binomialfordelinger i NetLogo
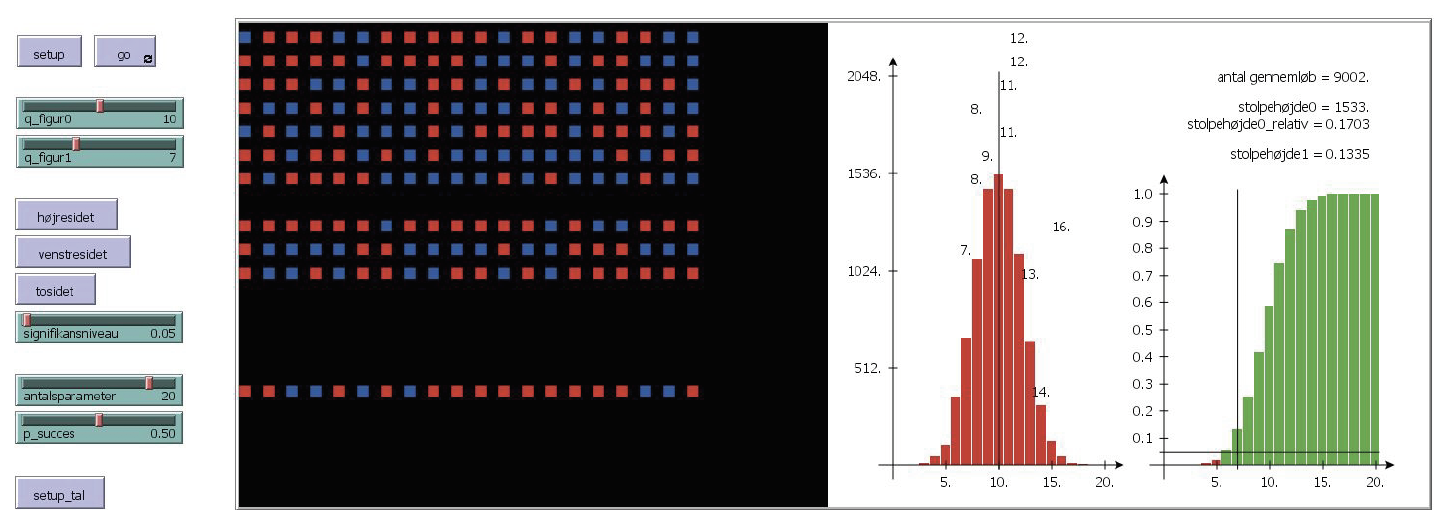
Introduktion I et forløb om sandsynlighed og kombinatorik har NetLogo-programmer været anvendt til at simulere binomialfordelinger med en rimelig grad af nøjagtighed. Eleverne har brugt
Fysik
Rækkevidde af skråt kast
Introduktion Rækkevidden af et skråt kast, når affyringen sker over eller under jordniveau har ingen simpel løsning. Dette, I modsætning til affyring fra jordniveau, hvor
